Lesson 2: 從函數計算與繪製開始

Objective :

學習數學函數的計算方式
數學函數的繪圖技術
更熟練 Python 的語法使用
熟練 markdown 的編輯技巧，參考語法。

Prerequisite:

了解物件型態（Object type） : Number, String, List, Tuple, Dictionary, File
懂得定義矩陣： np.linspace(), np.arange()

範例 1：繪製函數圖形 $f(x) = x^2 + 3x + 5,\;\; -5 \leq x \leq 5$

重點提示：

練習 Jupyter Notebook 的 markdown 編輯，含文字與數學式。
開始熟悉 matplotlib 的基本函數繪圖。

注意事項:

Python 有幾個著名的繪圖套件，如 matplotlib, seaborn, plotly, pyqtgraph…等，各擅勝場。這些套件都非常龐大，功能甚多，較難同時學習。在此選擇從 matplotlib 開始熟悉，若不足之處再考慮加入其他套件。

開始使用 matplotlib 套件並熟悉其繪圖指令與技巧。
基本的函數繪製方法：
- 先設定 n 個 x 值（向量）np.linspace()
- 計算每個 x 值的函數值 y (向量）
- 繪製 n 個座標 (x, y)
使用了座標區格線，加入 x 軸與 Y 軸的標籤文字。
加入抬頭 title 並以 LaTeX 的數學式呈現。
學習在 ipynb 檔製作 markdown 文字、數學式及各種排版，如圖一與二。

import matplotlib.pyplot as plt
import numpy as np

n = 100 # number of points
# create a x vector
x = np.linspace(-5, 5, n) 
# compute y
y = x**2 + 3*x + 5
 
plt.plot(x, y)
plt.grid(True)
plt.xlabel('X')
plt.ylabel('Y')
plt.title('$f(x)=x^2+3x+5$')
plt.show()  # just for py file

範例 2：繪製函數圖形 $f(x) = x^3 - 10x^2 + 29x - 20,\;\; 0 \leq x \leq 7$

重點提示：

匿名函數的使用： lambda x:
擴增 matplotlib 的能力，譬如 figure, 更細膩的 grid, 線條型態 linestyle、粗細 linewidth 與顏色 color。

注意事項:

使用 np.arange() 定義 X 變數值
使用 numpy 的匿名函數定義（anonymous function）: lambda.
使用 plt.figure() 先建立空白圖形並預先設定圖形長寬規格
開始加入函數線條的變化，如線的型態（linestyle）與顏色(color)

import matplotlib.pyplot as plt
import numpy as np

x = np.arange(0, 7, 0.01) 
# formulate a function f
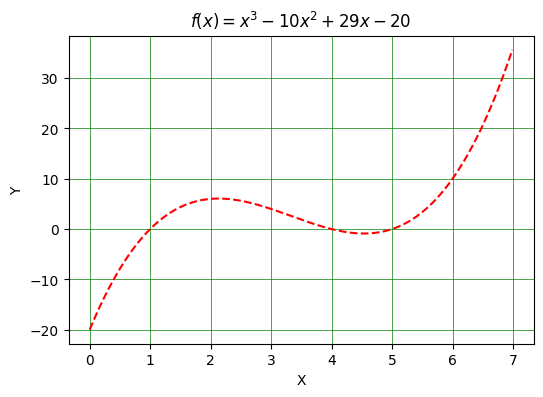
f = lambda x : x**3 - 10*x**2 + 29*x - 20

fig = plt.figure(figsize=[6, 4])
plt.plot(x, f(x), linestyle = '--', color = 'r')
plt.grid(visible = True, color='g', linestyle='-', linewidth=0.5)
plt.xlabel('X'), plt.ylabel('Y')
plt.title('$f(x)=x^3-10x^2+29x-20$')
plt.show()

範例 3：繪製函數圖形 $f(x) = x^4 - 8x^3 + 16x^2 - 2x +8$

重點提示：

使用 numpy 多項式函數 polyval
使用 axis 繪圖並存成圖檔。
謹慎處理繪圖的範圍選擇。不當的範圍將錯過許多視覺資訊。
使用 latex 語法於繪圖區，譬如 title 與作圖區任何位置。

注意事項:

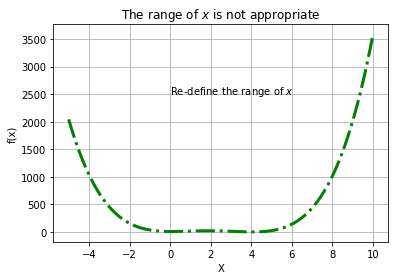
繪製函數圖形必須留意 X 變數的範圍，方能呈現出函數的內涵，譬如相對與絕對極值、函數是否與 y=0 相切、漸近線…等。譬如，下方附圖刻意示範一個不好的 X 值範圍，造成中間可能存在函數豐富的變化，卻被兩邊非常大的函數值「剷平」（視覺上），因此必須在縮小範圍，直到浮現函數該有的面貌為止。
使用 numpy 的 polyval 計算多項式函數值，讓程式更簡潔。
使用圖形的座標軸物件（ax=plt.gca()）來繪製函數圖（ax.plot()），有別於前面範例使用圖形物件 plt.plot()。當一個圖形（figure）只含一個座標軸（axes）時，使用 ax.plot() 與 plt.plot() 的結果都一樣，差別只是使用的指令稍有不同。當一個 figure 含有多個 axes 時，即一張圖內含多張子圖，則 axes 以矩陣的方式代表不同子圖的座標軸。詳見後面的範例。
加入函數線的寬度（linewidth）與 plt.text() 在座標區域內加入文字或數學式
加入儲存圖形檔的指令，並示範以 eps 格式儲存.

import matplotlib.pyplot as plt
import numpy as np

xmin, xmax = -5, 10
x = np.linspace(xmin, xmax, 100)
p = [1, -8, 16, -2, 8]
f = lambda x : np.polyval(p, x)

fig = plt.figure()
# use axis object
ax = plt.gca() # get current axis
ax.plot(x, f(x), linewidth = 3, color ='g', linestyle ='-.')
ax.grid(True)
ax.set_xlabel('X'), ax.set_ylabel('f(x)')
ax.set_title('The range of $x$ is not appropriate')
# ax.text(0, 2500, 'Re-define the range of $x$')
# save the current figure as an eps file
plt.savefig('poly.eps', format='eps')
plt.show()

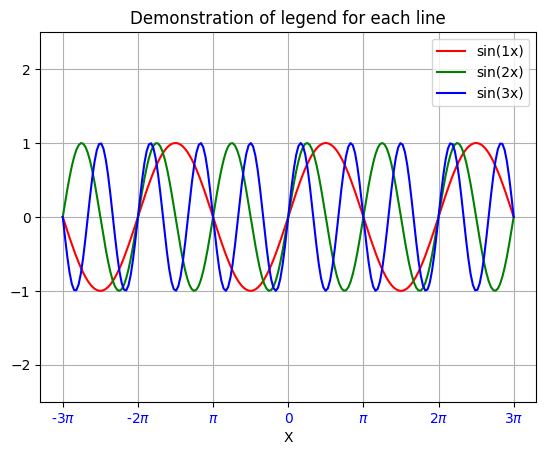
範例 4: 將下列三個函數繪製在同一個座標區並以 legend 標示區別。
$f_1(x) = \sin x, \; f_2(x) = \sin 2x, \;\; f_3(x) = \sin 3x$

重點提示：

加入函數線條的 legend。
熟悉文字與變數的組合： format。

注意事項:

由於上述函數具規則性，因此可以用迴圈繪製。
初學者第一次碰到沒用過的數學函數與常數如 of $\sin x$ and $\pi$ ，最好上網至官網（numpy）查詢，學習看懂使用說明，並學習官網的範例。
示範在迴圈中加入每個線條的顏色。顏色必須先設定。
示範如何在繪製每個圖形時，使用標籤 label 文字，才能在最後加入 plt.legend() 呈現圖形說明文字。
程式也示範如何在迴圈中組合文字與動態的數字，如 label = ‘sin({}x)’.format(i).

示範利用座標區物件來設定特定的 X 軸刻度（xtick) 與刻度的代表文字（ ticklabel），請注意：X 軸刻度與刻度的代表文字無法以 plt 設定。下列程式碼以 plt.subplots(1) 取得座標區物件。

import numpy as np
import matplotlib.pyplot as plt

n = [1, 2, 3]
colors = ["r", "g", "b"]
x = np.linspace(-3 * np.pi, 3 * np.pi, 200)
fig, ax = plt.subplots()
for i in n:
    y = np.sin(i * x)
    ax.plot(x, y, label="sin({}x)".format(i), color=colors[i - 1])

ax.legend()
ax.grid(True)
plt.xlabel("X")
ax.set_ylim([-2.5, 2.5])
ax.set_xticks(np.array([-3, -2, -1, 0, 1, 2, 3]) * np.pi)
ax.set_xticklabels(
    ["-3$\pi$", "-2$\pi$", "$\pi$", "0", "$\pi$", "2$\pi$", "3$\pi$"],
    fontsize=10, color="b")
ax.set_title("Demonstration of legend for each line")
plt.show()

範例 5 : 繪製函數圖形 $f(x) = \frac{4}{\pi}(\sin x + \frac{\sin 3x}{3} + \frac{\sin 5x}{5} + \frac{\sin 7x}{7} + \cdots)$

重點提示：

利用迴圈技術處理函數的無限項次計算。
使用 subplots 製作不同排列的子圖。

注意事項:

初學者應先模仿前面的範例程式，試著自己 coding。
這個函數有無線項次，開始寫程式時，最好一項一項加進來執行繪圖，成功了，再來嘗試迴圈的做法。
在實務面上，不可能做到無限項次，而是代之以足夠數量的有限項次。
加入調整 Y 軸座標範圍的指令 ax.set_ylim 或 plt.ylim()

圖一展示最簡單的單一子圖（等於原圖），使用 subplots(1) 指令。

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-3 * np.pi, 3 * np.pi, 200)
y = 4 / np.pi * (np.sin(x) + np.sin(3 * x) / 3 + np.sin(5 * x) / 5)

fig, ax = plt.subplots(1)
ax.plot(x, y, color="b")
ax.set_xticks(np.array([-3, -2, -1, 0, 1, 2, 3]) * np.pi)
ax.set_xticklabels(
    ["-3$\pi$", "-2$\pi$", "$\pi$", "0", "$\pi$", "2$\pi$", "3$\pi$"],
    fontsize=10,
    color="b",
)
ax.set_ylim([-3, 3])
ax.grid(True)
ax.set_title("Add three terms")
plt.show()

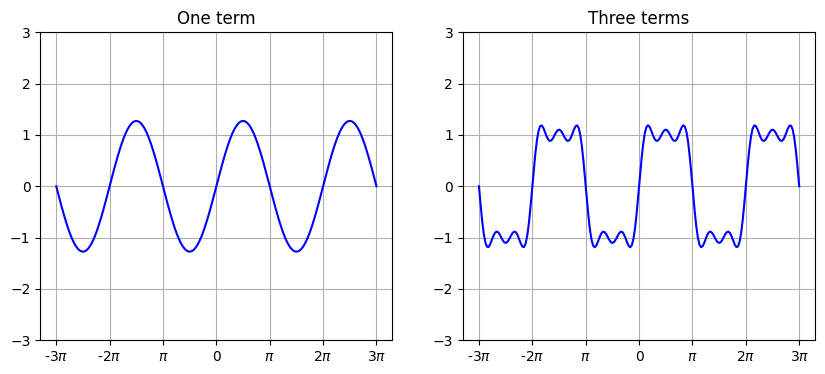
圖二展示排列為 1 x 2 的子圖，使用 subplots(1, 2) 指令。此時輸出的座標軸物件 ax 為一向量。

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-3 * np.pi, 3 * np.pi, 200)
y1 = 4 / np.pi * np.sin(x)
y3 = 4 / np.pi * (np.sin(x) + np.sin(3 * x) / 3 + np.sin(5 * x) / 5)

fig, ax = plt.subplots(1, 2, figsize=(10, 4))
ax[0].plot(x, y1, color="b")
ax[0].set_xticks(np.array([-3, -2, -1, 0, 1, 2, 3]) * np.pi)
ax[0].set_xticklabels(
    ["-3$\pi$", "-2$\pi$", "$\pi$", "0", "$\pi$", "2$\pi$", "3$\pi$"],
    fontsize=10,
    color="k",
)
ax[0].set_ylim([-3, 3])
ax[0].grid(True)
ax[0].set_title("One term")
ax[1].plot(x, y3, color="b")
ax[1].set_xticks(np.array([-3, -2, -1, 0, 1, 2, 3]) * np.pi)
ax[1].set_xticklabels(
    ["-3$\pi$", "-2$\pi$", "$\pi$", "0", "$\pi$", "2$\pi$", "3$\pi$"],
    fontsize=10,
    color="k",
)
ax[1].set_ylim([-3, 3])
ax[1].grid(True)
ax[1].set_title("Three terms")
plt.show()

圖三展示排列為 2 x 2 的子圖，使用 subplots(2, 2) 指令。此時輸出的座標軸物件 ax 為一 2 x 2 的矩陣。

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-3 * np.pi, 3 * np.pi, 200)
y1 = 4 / np.pi * np.sin(x)
y2 = 4 / np.pi * (np.sin(x) + np.sin(3 * x) / 3)
y3 = 4 / np.pi * (np.sin(x) + np.sin(3 * x) / 3 + np.sin(5 * x) / 5)
y4 = 4 / np.pi * (np.sin(x) + np.sin(3 * x) / 3 + np.sin(5 * x) / 5 + np.sin(7 * x) / 7)

fig, ax = plt.subplots(2, 2, figsize=(10, 8))
ax[0][0].plot(x, y1, color="b")
ax[0][0].set_ylim([-3, 3])
ax[0][0].grid(True)
ax[0][0].set_title("One term")
ax[0][1].plot(x, y2, color="b")
ax[0][1].set_ylim([-3, 3])
ax[0][1].grid(True)
ax[0][1].set_title("Two terms")
ax[1][0].plot(x, y3, color="b")
ax[1][0].set_ylim([-3, 3])
ax[1][0].grid(True)
ax[1][0].set_title("Three terms")
ax[1][1].plot(x, y4, color="b")
ax[1][1].set_ylim([-3, 3])
ax[1][1].grid(True)
ax[1][1].set_title("Four terms")
plt.show()

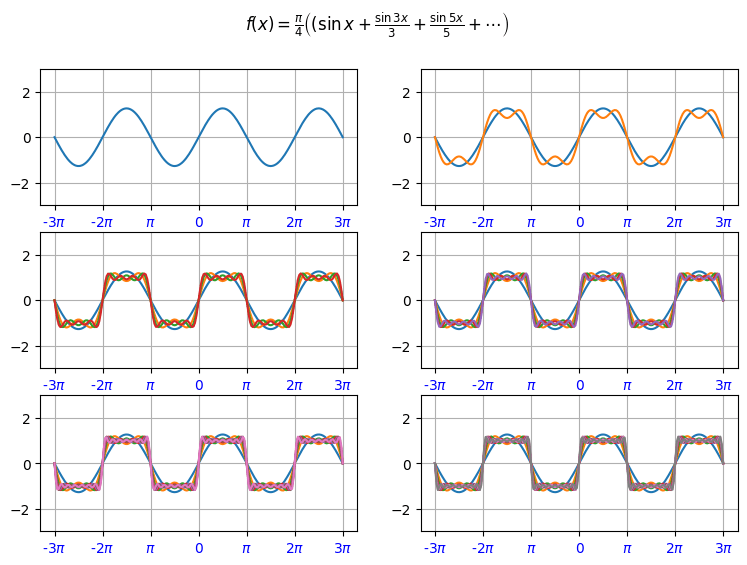
圖四用雙迴圈分別處理行與列的子圖，以便能擴充至任意排列。圖中的 title 以 plt.suptitle() 製作，即 super title 之意。

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-3 * np.pi, 3 * np.pi, 200)
rows, cols = 3, 2
fig, ax = plt.subplots(nrows=rows, ncols=cols, figsize=(9, 6))
for i in range(rows):
    for j in range(cols):
        axtmp = ax[i][j]
        n = i * rows + j + 1
        y = 0
        for k in range(n):
            l = 2 * k + 1
            y = y + np.sin(l * x) / l
            axtmp.plot(x, 4 * y / np.pi)
            axtmp.set_xticks(np.array([-3, -2, -1, 0, 1, 2, 3]) * np.pi)
            axtmp.set_xticklabels(
                ["-3$\pi$", "-2$\pi$", "$\pi$", "0", "$\pi$", "2$\pi$", "3$\pi$"],
                fontsize=10,
                color="b",
            )
            axtmp.set_ylim([-3, 3])
            axtmp.grid(True)

plt.suptitle(
    "$f(x) = \\frac{\pi}{4}\\left((\sin x+\\frac{\sin 3x}{3}+\\frac{\sin 5x}{5}+\cdots\\right)$"
)
plt.show()

製作出同圖四的子圖，但只使用一個迴圈來處理行列的排列問題。關鍵是將行列打平為一向量（axs.flat）並用 enumerate() 註記每個位置的座標軸順序 i 與對應的座標軸物件 ax。順序的排法從左至右，由上而下。這種處理排列圖案的方式較為簡潔。

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-3 * np.pi, 3 * np.pi, 200)
rows, cols = 3, 2
fig, axs = plt.subplots(rows, cols, figsize=(9, 6))
for i, ax in enumerate(axs.flat):  # flat: 1D iterator over the array
    n = i + 1
    y = 0
    for k in range(n):
        l = 2 * k + 1
        y = y + np.sin(l * x) / l
        ax.plot(x, 4 * y / np.pi)
        ax.set_xticks(np.array([-3, -2, -1, 0, 1, 2, 3]) * np.pi)
        ax.set_xticklabels(
            ["-3$\pi$", "-2$\pi$", "$\pi$", "0", "$\pi$", "2$\pi$", "3$\pi$"],
            fontsize=10,
            color="b",
        )
        ax.set_ylim([-3, 3])
        ax.grid(True)
plt.suptitle(
    "$f(x) = \\frac{\pi}{4}\\left((\sin x+\\frac{\sin 3x}{3}+\\frac{\sin 5x}{5}+\cdots\\right)$"
)
plt.show()

範例 6: 繪製補滿（patch）顏色的多邊形

重點提示：

加入正方形即塗色：patch。
使用 axis 繪圖。

注意事項:

這裡使用了 matplotlib 套件中的 patches 模組。模組裡有一個指令 Rectangle 能畫出長方形。若要畫多邊形，請參考 matplotlib 使用手冊關於 polygon 的使用方式。
特殊形狀的圖形被視為一個物件，因此以 add_patch() 的方式加入座標區。
關於 Rectangle 的使用方式，可以根據程式碼與圖形結果去猜測。若想進一步了解，立刻翻閱手冊。
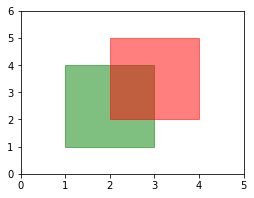
下圖的顏色搭配了透明度（transparency），呈現半透明（alpha=0.5）。請試著改變透明度，看看其他效果。

import matplotlib.pyplot as plt 
import matplotlib.patches as pat

fig, ax = plt.subplots(figsize=(4,3))
rec1 = pat.Rectangle((1, 1), 2, 3, color ='green', alpha = 0.5)
ax.add_patch(rec1)
rec2 = pat.Rectangle((2, 2), 2, 3, color ='red', alpha = 0.5)
ax.add_patch(rec2)
plt.xlim([0,5]), plt.ylim([0,6])
plt.show()

範例 7: 繪製下列兩個函數圖，並函數所夾的區域塗上顏色

$f(x) = 2x-x^2,\;\; g(x) = x^2$

重點提示：

在函數之間塗色：fill_between。
變更座標軸的位置。
在座標軸區域塗顏色。
使用 annotate 線條。

注意事項:

這是微積分常見的題目。請任選微積分課本的題目，練習為兩函數包圍的區域塗上顏色。盡量挑選有挑戰性的函數，程式技巧才會進步。
指令 fill_between 的語法，請自行從指令中猜測。並且嘗試做出各種選項（呈現包圍之外的區域）。
這個程式也示範了如何調整座標區的四個座標軸（上下左右）。使用方式請自行猜測，並嘗試改變並觀察結果。
本程式也示範了在座標區域寫上數學式並拉一條帶箭頭的標示線只到特地位置的 annotate 技巧。
座標區可以交由 ax.set_facecolor 控制顏色。

import numpy as np 
import matplotlib.pyplot as plt 

x = np.linspace(-0.5, 1.6, 100)
f = lambda x : 2*x - x**2
g = lambda x : x**2

plt.plot(x, f(x), x, g(x)) # draw two lines in a command
plt.fill_between(x, f(x), g(x), where = f(x) > g(x), color = 'pink') # defaut : y1>y2
ax = plt.gca()
# Re-arrange four axes spines
ax.spines['left'].set_position(('data',0))
ax.spines['bottom'].set_position(('data',0))
ax.spines['top'].set_visible(False) # take off top line
ax.spines['right'].set_visible(False)
ax.set_facecolor('#D5FAF9')
ax.annotate('$\int_0^1 (f(x) - g(x)) \; dx$', \
    xy=(0.5, 0.5), xytext=(0.3, 1.5), \
        arrowprops=dict(arrowstyle='->', \
            connectionstyle='arc3, rad=0.3'), fontsize =14)
plt.show()

習題 :

注意事項:

畫出下列函數，X 軸範圍自訂，盡量畫出最完整的函數圖，能呈現隱藏在函數的資訊。
將上述範例介紹的繪圖技巧充分地應用，讓自己熟悉各種繪圖的表現，包括文字、刻度、顏色、legend、grid、座標軸的位置… 等。不是只將函數畫出來而已，還要畫得好。有些函數需要的指令不在前面的範例，請自行上網查詢手冊。

Exercises:

$\displaystyle f(x) = \frac{\sin(x)}{x}, \;-3\pi \leq x \leq 3\pi$ ，並從圖猜測 $\lim_{x\rightarrow 0} f(x) = ?$ 再加入第二與第三個函數 $\displaystyle g(x) = \frac{\sin(x^2)}{x}, h(x) = \frac{\sin^2(2x)}{x^2}$ ，同時猜測 $\lim_{x\rightarrow 0} g(x) = ?, \lim_{x\rightarrow 0} h(x) = ?$
$\displaystyle f(x) = \frac{e^{\alpha x}}{e^{\alpha x} + 1}, \alpha=1$ ，畫出漸近線與函數爬升的趨勢。
$f(x) = e^{-x/10} \sin(x)$ ，畫出震盪幅度逐漸變小的趨勢。
$f(x) = \displaystyle\frac{1}{x-2}$ ，畫出漸近線的趨勢。分母為 0 的計算會引發警告，可以在設定 x 軸範圍時避開。譬如， np.setdiff1d(np.linspace(-5, 5, 200),[0])
$f(x) = x^3 + 2$ ，繪製 $f(x)$ 與 $f^{-1}(x)$ 在同一張圖上並展示其互為反函數的對稱性。
$\displaystyle f(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{(x-3)^2}{2}}$ ，畫出這張知名圖形的特色。
$f(x) = 3x^3-x^4$ ，透過 X 軸範圍的選擇，觀察函數是否有最大值？是否看得出函數有幾個實數根？
$f(x) = \frac{\ln x}{x^2}$ ，圖形必須清楚地呈現出最大值的大概位置與右邊漸近線的趨勢。
$f(x) = \begin{cases}1, & 1 \leq x < 3 \\2, &3 \leq x < 5 \\3, &5 \leq x < 7 \end{cases}$
.

圖形如下左圖。畫圓可以這樣做：
- 第一種方法：將變數 x 與 y 表示為另一個變數 $\theta$ 的函數, i.e. $x = \sin \theta, y = \cos \theta, \;\; 0 \leq \theta \leq 2\pi$
- 第二種方法：將圓形方程式當作隱函數（implicit function）處裡。必須找到適當的指令。
- 第三種方法：去 matplotlib 套件的手冊找找看，有沒有畫圓的指令。
但不管採取何種方式，最後都要將座標軸設定為等寬模式，看到的圓才比較「圓」，否則即使做對了，看起來還是像橢圓。如果採座標區物件的繪圖方式，可以用指令 ax.set_aspect(1) 將座標區域變成方形。
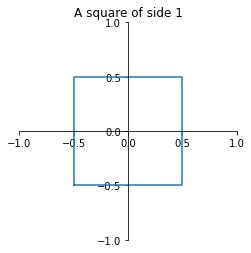
繪製如下右圖的正方形。可以展示多種繪圖方式。

Project : Comparison Theorem

Let $S_n=\sum_{k=1}^{n} \frac{1}{k}=1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}$

Verify that $\lim_{n\rightarrow \infty} S_n$ diverges.
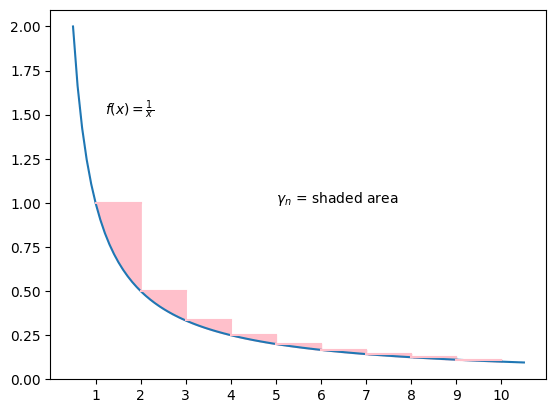
Let $\gamma_n$ denote the sum of the shaded areas as shown in 圖一. Show that $\gamma_n=S_n-\ln (n+1)$ （可以直接證明）
Verify that $\frac{1}{2}(1-\frac{1}{n+1})<\gamma_n < 1$ . (Hint: To show this inequality, it can be done by comparing each shaded area with a larger rectangle and a smaller triangle.)

注意事項：

這些問題都可以證明（show），不過在此以驗證（verify）取代，也就是用程式計算的結果來逼近真實情況。譬如 (1) 的發散（diverge）可以嘗試改變 $n$ ，從小變大直到很大很大，如 $n=100, 1000, \cdots, 10^6, \cdots$ 並計算 $S_n$ ，觀察其數值的變化。最好能列印出 $n$ vs. $S_n$ ，並繪製圖形，方便觀察。
問題 2 的證明在 markdown 記錄下來。
問題 3 可以畫一張圖展示 $n$ vs. $\gamma_n, \frac{1}{2}(1-\frac{1}{n+1})$ ，如圖二，其中 $\gamma_n$ 一直處於中間位置。
學習寫程式計算統計問題，最好多做一些這類的小專題，較能學用合一，懂得程式語言用在哪裡、該加強哪一部分。另一方面也會對統計或數學問題有更深一層的體會。