汪群超 Chun-Chao Wang

Dept. of Statistics, National Taipei University, Taiwan

SML/Lesson 5: 主成分分析的原理與實驗

下載本文所需檔案：city_quality.xlsx, son.txt & football.txt

Py_BOOK_PCA_Fundamental下載

參考文章：

  1. A Step-by-Step Explanation of Principal Component Analysis (PCA)
  2. 世上最生動的 PCA：直觀理解並應用主成分分析

習題 1：有一組資料來自義大利某個地區三個紅酒製造商所產的紅酒，資料內容包括的 178 支紅酒的 13 種化學成分。利用這組資料回答下列問題：（下載 Wine.xlsx）

  1. 觀察資料。譬如利用 pandas 的 head() 指令呈現前面幾筆資料。

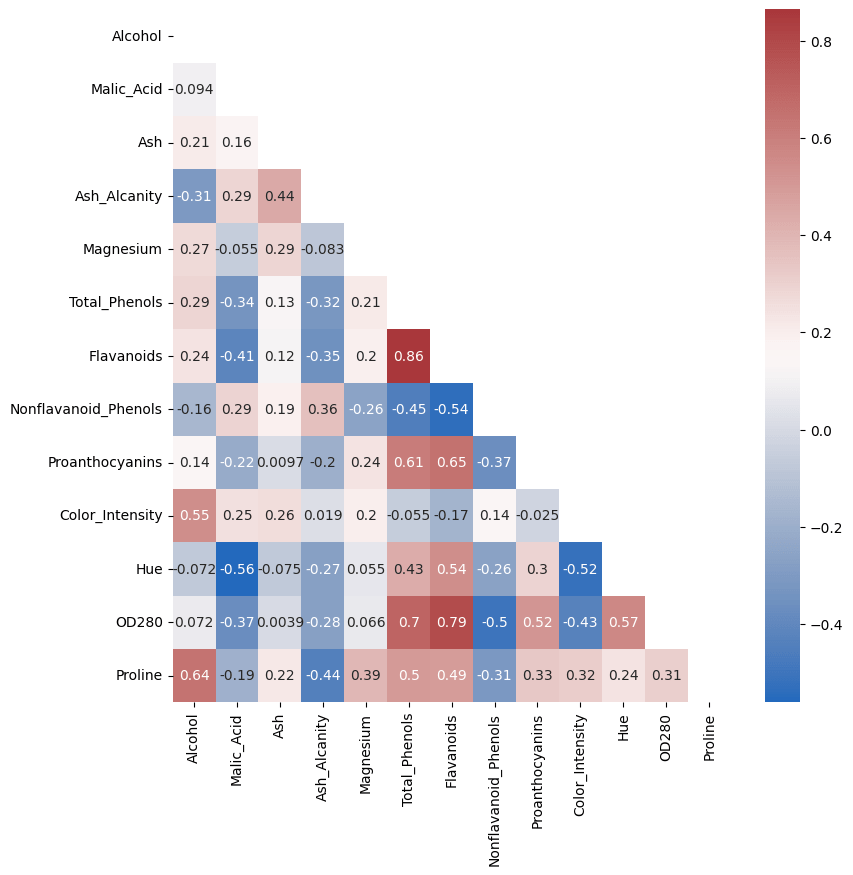
  2. 繪製變數間的相關係數圖，以觀察變數間是否存在相關性，參考如圖一（或其他類似的圖）。

  3. 繪製一張含每個化學成分（變數）的盒鬚圖（Boxplot），觀察每個變數的 scaling，作為是否標準化的參考，參考如圖二。

  4. 進行主成分分析，繪製特徵值由大而小的分布與 scree plot。參考如圖三。

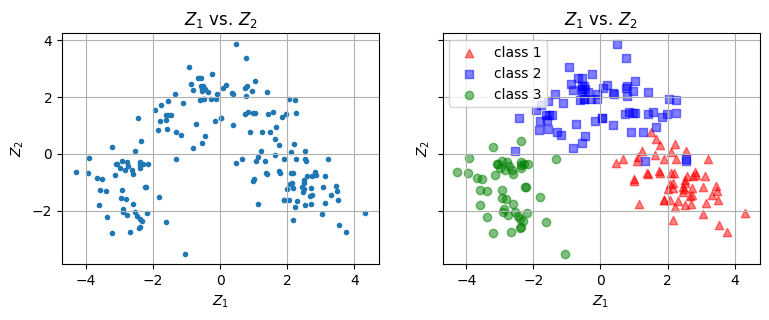
  5. 資料中的每支酒都有標籤（label），代表來自哪個酒莊。假設先不看這項標籤。利用主成分分析取得前兩項成分，並繪製其散布圖。如圖四（左）。是否可以從兩個主成分的散布圖中看出三個群組？請注意：資料是否先做標準化可能會影響結果，試著觀察做與不做標準化的差別。

  6. 再依據每個資料的標籤，為每個在散布圖上的資料點塗上顏色，如圖四（右）。

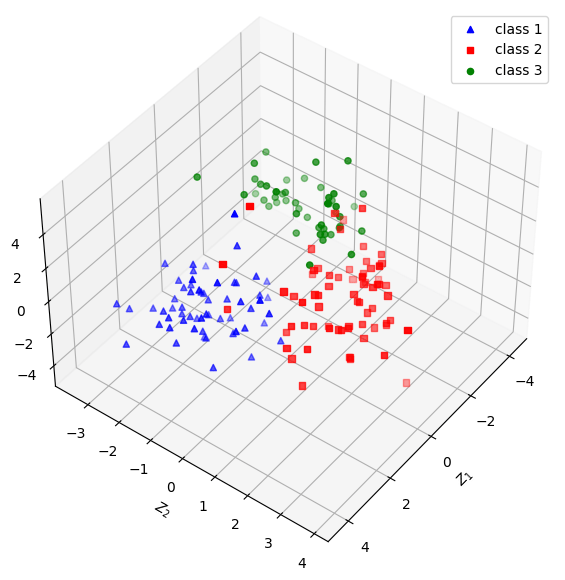
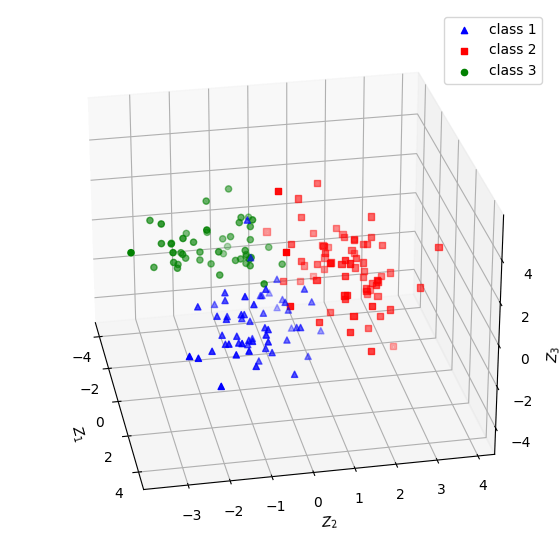
  7. 如果採三個主成分，則可繪製如圖五與圖六的立體圖。觀察圖五、六是否比圖四（右）具備更好的群組分辨能力。請嘗試旋轉立體圖的角度以取得最好的辨別視野。

  8. Z_1 與 Z_2 都是從原變數組合而成的新變數，可否從 Z_1 與 Z_2 的組成係數（即前兩個 eigenvector 的值），看出原變數哪個比較重要？哪個比較不重要？若再與原變數間的相關係數圖對照，是否透露相同的訊息。先不管理論怎麼說，就只是談談你的觀察與猜測。（譬如可以畫 eigenvectors 與變數對應的 heatmap）。

建議先自己嘗試回答以上問題，再參考 sklearn 網站的範例程式與說明。

圖一、變數間的相關係數矩陣圖
圖二、盒鬚圖（Boxplot）：（左）原資料，（右）標準化資料。
圖三、（左）每個主成分對變異數的解釋（特徵值）與（右）累積的解釋變異數。
圖四、前兩個主成分：（左）未加註群組顏色與（右）加註群組顏色與符號。
圖五、考慮三個主成分的散布圖：角度 1
圖六、考慮三個主成分的散布圖：角度 2

習題 2：回答類似習題 1 的問題（如下所述），資料來自 NUMBEO 的 Quality of Life Index by City 2025 （下載 2025_city_quality.xlsx）關於世界 263 個城市的生活品質排名，其中包含 8 個指標數字。在此可以將排名資料置換成代表生活品質的「標籤 labels」，譬如總分數（欄位 Quality of Life Index）200 分以上稱為「高品質」或「HIGH」，並配與數字 3；分數 100 ~200 稱為「中品質」或「MEDIUM」，並配與數字 2；總分 100 以下稱為「低品質」或「LOW」，並配與數字 1。當然這種分組方式可以自訂，譬如分四組或五組，再看看進行 PCA 後的表現。

  1. 觀察資料。譬如利用 pandas 的 head() 指令呈現前面幾筆資料。

  2. 繪製變數間的相關係數圖，以觀察變數間是否存在相關性（參考上題的圖或其他類似的圖）。

  3. 繪製一張含每個量測變數的盒鬚圖（Boxplot），觀察每個變數的 scaling，作為是否標準化的參考（如上題繪製的兩張 Boxplot 圖, 一張針對原始資料，另一張則是標準化後的資料）。

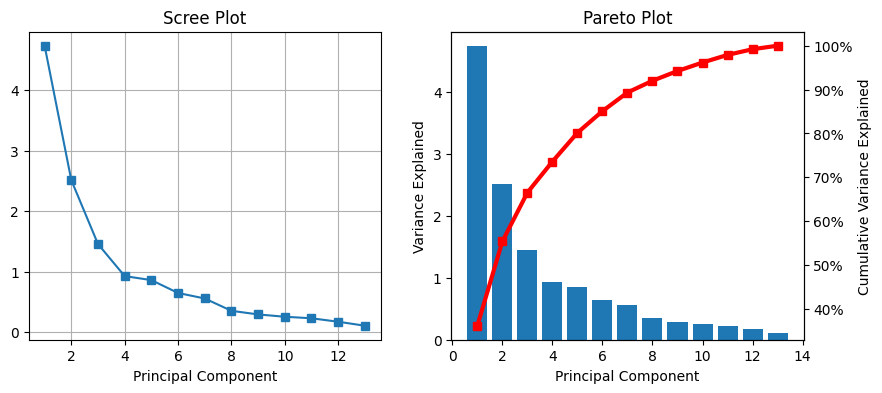
  4. 進行主成分分析，繪製特徵值由大而小的分佈，如 scree plot 與累積百分比的 pareto plot。

  5. 每筆資料都有標籤值（label），代表生活品質的高低（3: HIGH, 2:MEDIUM, 1:LOW）。假設先不看這項標籤。利用主成分分析取得前兩項成分（Z_1 與 Z_2），並繪製其散佈圖。是否可以從兩個主成分的散佈圖中看出兩個群組？請注意：資料是否先做標準化可能會影響結果，試著觀察「做與不做」標準化的差別。

  6. 再依據每筆資料的標籤（可以配以適當的文字，譬如 3 配置 HIGH），在散佈圖上塗上不同顏色（參考上題的圖）。

  7. 從 Z_1 與 Z_2 的散佈圖進一步推敲，也許需要加入 Z_3 才能分得更好，又或許去除 Z_2 僅取 Z_1 也可以分得不錯。請提出你的看法。

  8. Z_1 與 Z_2 都是從原變數組合而成的新變數，可否從 Z_1 與 Z_2 的組成係數（即前兩個 eigenvector 的值），看出原變數哪個比較重要？哪個比較不重要？若再與原變數間的相關係數圖對照，是否透露相同的訊息。先不管理論怎麼說，就只是談談你的觀察與猜測。（譬如可以畫 eigenvectors 與變數對應的 heatmap）

習題 3：回答類似習題 1 的問題（如下所述），資料則是同樣來自 sklearn.datasets 的一組關於乳癌患者腫瘤的影像量測資料。量測變數共 30 個，樣本數為 569 位患者，區分為兩個群組，分別是 Malignant（惡性腫瘤）與 Benign（良性腫瘤）。請注意，由於變數多，因此如前一練習的相關性圖，必須做些改變。

資料的細節與下載方式詳見： sklearn.datasets.load_breast_cancer

  1. 觀察資料。譬如利用 pandas 的 head() 指令呈現前面幾筆資料。

  2. 繪製變數間的相關係數圖，以觀察變數間是否存在相關性（參考上題的圖或其他類似的圖）。

  3. 繪製一張含每個量測變數的盒鬚圖（Boxplot），觀察每個變數的 scaling，作為是否標準化的參考（如上題繪製的兩張 Boxplot 圖, 一張針對原始資料，另一張則是標準化後的資料）。

  4. 進行主成分分析，繪製特徵值由大而小的分佈，如 scree plot 與累積百分比的 pareto plot。

  5. 每筆資料都有標籤值（label），代表腫瘤的成分（Malignant（惡性腫瘤）或 Benign（良性腫瘤））。假設先不看這項標籤。利用主成分分析取得前兩項成分，並繪製其散佈圖。是否可以從兩個主成分的散佈圖中看出兩個群組？請注意：資料是否先做標準化可能會影響結果，試著觀察「做與不做」標準化的差別。

  6. 再依據每筆資料的標籤，在散佈圖上塗上不同顏色（參考上題的圖）。

  7. 如果採三個主成分，則可繪製立體圖。請嘗試旋轉立體圖的角度以取得最好的辨別視野。

  8. Z_1 與 Z_2 都是從原變數組合而成的新變數，可否從 Z_1 與 Z_2 的組成係數（即前兩個 eigenvector 的值），看出原變數哪個比較重要？哪個比較不重要？若再與原變數間的相關係數圖對照，是否透露相同的訊息。先不管理論怎麼說，就只是談談你的觀察與猜測。（譬如可以畫 eigenvectors 與變數對應的 heatmap）

商學院  7F16
ccw@gm.ntpu.edu.tw
(02)8674-1111 
ext 66777

部落格統計

  • 211,257 點擊次數

Blog at WordPress.com.